Thoughts as Computation

What is the difference between human and computer memory? A typical answer is: computer memory is essentially a long sequence of bytes (although, there are exceptions), and to store any information, we only have the choice to store it further up or down the line. But human memory works with associations, and is also called content-addressable. One example is that if you see the face of somebody you know, you instantly recognise the person without having to "look through" the faces of people you know until you have found a match. Web search engines are a bit similar. They take some content, the search query, and return websites with similar meaning. A crucial difference between the two memory architectures is this: on a straight line, as in computer memory, drawing connections between elements is limited. By nature, any element on this line has at most two: with the elements left and right of it.

Meanwhile, we can connect ideas and concepts seemingly without limitation in our minds (this is probably one of the most fascinating things our minds are capable of, although it is not always emphasised in education). It has also been shown that we are most effective at learning new things when we can connect them to things we already know.

The structure of any text is similar to a computer's memory - both are essentially a long sequence of elements representing information. Yet, when reading a book, we can imagine the things described, reason about them and possibly even see connections and similarities among ideas, although the words describing them are separated by many other words or even pages. While reading a book, and absorb the words, parse their meaning and relate them to each other (given a sufficiently long attention span), the author's ideas re-emerge in our minds. What happened? Have we found a way to translate from computer memory to associative memory?

But if connecting things is a problem in the one-dimensional computer memory, how can we improve it? By adding dimensions, of course! For example, we can draw a (semantic) map of the concepts that we parsed in the text. Let us take this very text as example. In the figure below, a sentence from this text (1-D) is re-arranged (or embedded) into a semantic map (2-D). Where connections had to be created by linguistic constructs in the text (such as with relative pronouns or referring to names), we can arrange similar elements in similar parts of the space. Note that this is already easier to do than in with text, where each word only has two neighbours!

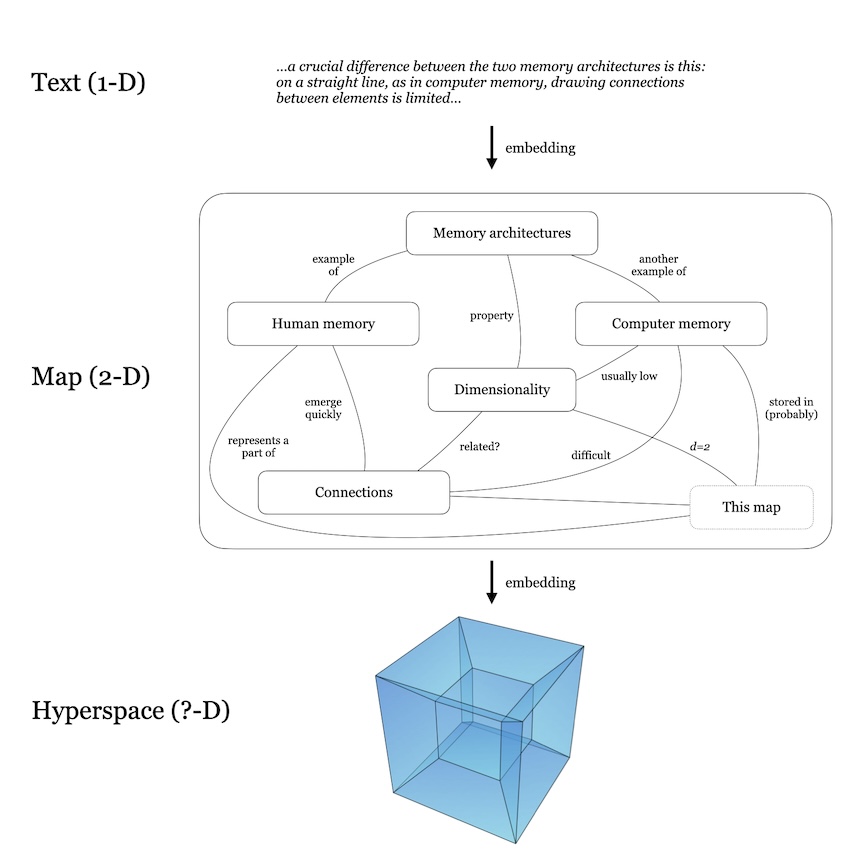
Connections emerge in higher dimensions

But even the 2-D space is limited - "Memory architectures" and "Connections" are far apart, although they have surely have connections. Even drawing lines becomes increasingly complicated with more elements (for text it would be even harder. Imagine a line from one word to another one that occurs several pages later). We can solve this problem by, of course, adding another dimension. In 3-D, every element can have six neighbours, and "Memory architectures" and "Connections" may simply be placed one above the other. (Another, topological trick would be to bend the diagram and connect the top with the bottom and the two elements would be close to each other.) We could now continue by adding more and more dimensions, moving into high-dimensional space (or Hyperspace) until we have found an embedding in which the concepts arranged just "right". But how large is the dimension? And are higher dimensions the answer to why our minds can see connections and similarities and reason about them?

The idea appears in similar form in Biology. For example, Proteins consist of long chains of amino acids, smaller molecules that act as building blocks. In this form they are called primary structures. Under the right conditions, the chains fold into a 3-D structure, with which they attain their biological function. The process can also be reverted. For example when cooking an egg, the 3-D structure of the contained protein unfolds again. Predicting the 3-D structure from the primary structure is a difficult problem, but recently, very successful new computational methods have been devised.

Embeddings

Connections can be modelled after several methods, and there is not a single correct way. Sometimes they are given by proximity, as trivially on a geographical map, and sometimes they are references, as with websites that use links to refer to other websites, more mathematically known as graph, and are very similar to networks. So wherever we explicitly know the connections, we can model them as a graph. For graphs, there are methods to embed them into a high-dimensional space. Although any graph can be embedded into 3-D space, this does not always make sense.

Alternatively, there is the approach of word embeddings, or their more general version, Thought vectors. Word embeddings have recently come in the focus of computer science since new ways to compute them. Essentially, they are vectors in hyperspace (100-1000 dimensions) and have the interesting properties that words with similar meaning are in similar regions and that the path from one vector to another carries meaning itself. For example, the path from the vectors /Rome/ to /Italy/ has the same direction as the one from /London/ to /United Kingdom/. In contrast to graph embeddings, a word embedding is created by examining the /context/ of the word. This context is relatively (i.e. up to few sentences) local, and will therefore not be able to encompass not so local meanings, or connections that span over many sentences. I argue that many inventions and discoveries could be made if these non-obvious connections, possibly requiring multiple jumps to other concepts, could be found. But how can such long-range connections be captured? Can thought vectors be combined with knowledge graphs, large graphs encompassing e.g. explicit knowledge about the world?

Small-world networks

The locality we encountered is typical for knowledge graphs, but different for e.g. social networks, or neural networks of worms (and probably other animals). The former type are called /regular/ networks, and the latter small-world networks. As illustrated below, small-world networks can be created from regular ones by simply connecting elements that are a bit further apart.

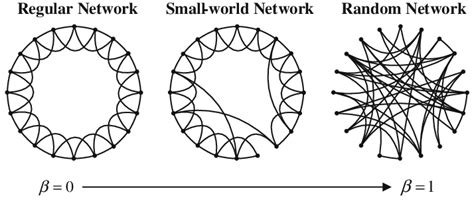
In such a network (or, graph), these shortcuts allow much shorter paths, e.g. when going from one side to another. In the case of knowledge graphs, I argue that it is exactly these shortcuts that create interesting connections. Such connections, for example, may unveil that methods developed for experimental Physics can be useful in Medicine, and found completely new research fields. There are many examples already, such as the adoption of biological neural networks in computer science, causing the current hype in AI, or the use of thermodynamics methods for artificially creating art.

Conclusion

I believe that not only topological, but also conceptual connections emerge within higher dimensions and that these connections are basis for much of our reasoning. When reading a text, we project the described information into a high-dimensional space, similar to graph, or word embeddings. As envisioned by others, I too think that these word embeddings are powerful for modeling thought as it occurs in our minds, but find that creating them only from their context is too limited because long-range connections are neglected. Long-range connections are found abundantly in nature and human structures, and may be one key for better modeling thoughts and making new discoveries, something current AI systems are lacking.